Note Processing for Guitar Effects

What's a "note"?

Seems like a silly question, because we can clearly hear notes in music, so it should be easy, right? While defining what a note is to a human might be easy, designing a circuit to pick out a note in a flow of music turns out to be surprisingly hard. Us human hearers happen to be probably the best pattern-matching intelligence on the planet, and we can readily dig audio signals out of noise and other bad conditions that would baffle instrumentation.

As effects makers, we are often interested in making something happen on a per-note basis. For instance, the quality of "sustain" is intimately tied to the length of a note. To get greater sustain, a note has to extend for a longer time without much change in its tonal qualities. The common sustainers manage to change the relative gain applied to signal, increasing it as the signal dies away. Auto-wah effects derive a signal that is proportional to the instantaneous loudness of a note, and change some property of a filter based on that loudness. Noise gates just determine when there is and is not a note, and turn the signal gain down to nil when there is no note playing. There are lots of other things we could do as tinkerers if we had a good way to extract information about notes from the flow of signal that comes out of a guitar.

Quite a lot of effects circuits come from a history with either organs or their souped up descendants, synthesizers. These instruments have the luxury of knowing exactly all the qualities of any given note, because they electronically synthesize the note itself. Guitar effects have a harder job because we can only determine things about notes while they are actually occurring, and have no information except the signal itself.

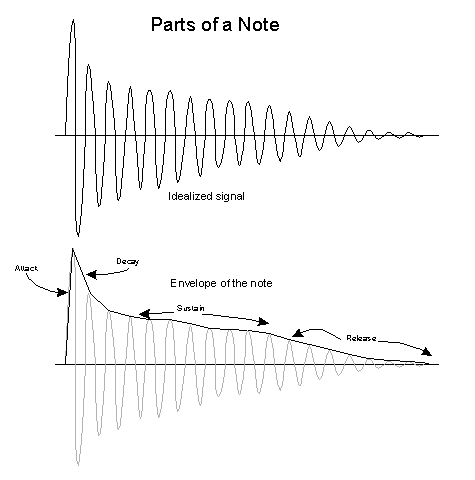So what's in a note? The sketch at left shows what might be an idealized version of an archetypical note. The very first signal we get, starting from nil, is a loud transient. This might correspond to the pick attack, when a guitar pick pulls the string massively further than it will vibrate normally. That initial loudness attack decays very quickly to the sustaining level of the note, where the note volume decays at a slower rate. When the musician ends the note, there may be other mechanisms that make the note sound for a little bit after the musician ended it. This is usually a much faster die off than the sustain part of the note.

The signal contains loudness information, frequency information, and in any real instrument harmonics and some noise. The simplified example does not do justice to a real guitar note, which is much less of a sine wave and more of a crooked sawtooth, at least in the simple case where only one note has been struck. If two or more strings have been played, both base frequencies and both sets of harmonics are present, and the supposed regularity gets really rough. Frequency and harmonics are very hard to extract useful info from, so almost all note processing goes for the amplitude envelope.

Organ and synth makers long ago standardized on the definitions of attack, decay, sustain, and release to describe the loudness dynamics of notes. All of these things are characteristics of normal acoustic instruments. For instance, horns have a very prominent attack/decay transient, known in the musicology biz as a "horn blip" - how's that for original? Some instruments have almost no attack transient, like a softly bowed violin. Some instruments have little or no release, well made electric guitars being one of them if you let the string simply ring until it dies out. However, on an acoustic guitar, even when you damp a ringing string, the sound it made reverberates inside the body cavity for a few milliseconds after the string stops moving, so there is a distinct release.

The bottom part of the sketch shows the envelope of the note. This is a hypothetical outline just touching the peaks of all the signal vibrations. Strict musical theory says that the envelope is two sided, top and bottom, but we're interested in electronic processing, so I'm going to only work with one half. In any case, the envelope represents at every instant the loudness of the note.

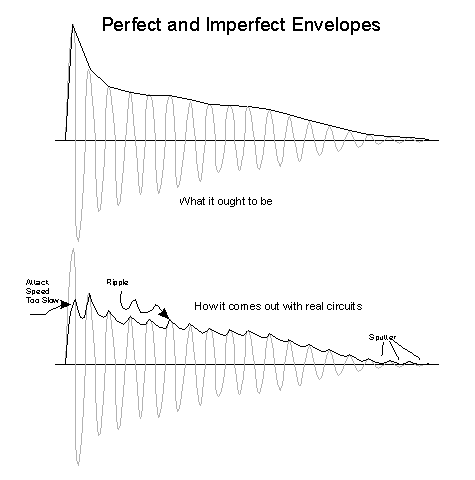It turns out that generating a perfect outline of any note is hard. The commonest thing to do is to half wave rectify the signal with an electronic precision rectifier. The sketch at left shows what you'd like to get versus what you actually might get in actual circuits.

Practical envelope generation circuits have to filter the rectified envelope to get the envelope not to sag between peaks in the signal. That filtering also slows down sensing the attack. Filtering ripple and having fast attack response are diametrically opposed, so there is often a compromise in practical circuits for losing some attack and enduring some ripple.

This compromise hurts at the end of a note as well, where the ripple might sag below the point where the circuit thinks there is a note, then get pushed up by the next peak. This can make for some sputtering uncertainty about the end of a note.

It helps to full wave rectify the signal. This flips the negative peaks up so that they charge the envelope filter between the positive peaks. This cuts the ripple on the detected envelope in half, allowing less filtering and therefore quicker response to the real instantaneous loudness.

There is even a double fullwave rectification technique that first full wave rectifies the signal, then blocks out the DC component and full wave rectifies the already full-wave signal. That effectively quadruples the peak frequency compared to the original signal and dramatically improves the ability to follow transients while still reducing ripple. The point of all this is to get an accurate "outline" of the loudness of the note at any moment.

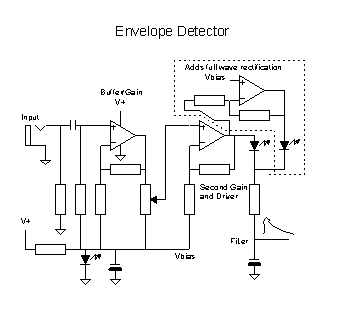One practical circuit for generating an envelope is shown at left. This is a cleaned up and fortified version of the envelope detector in simple auto-wahs like the Seamoon Funk Machine or the EH Dr. Q. The first amplifier buffers the raw signal and adds some gain - raw guitar signals are usually too small for good envelope signals, so we have to multiply them up a bit. The bias voltage for the first amp is generated either by an LED or a string of diodes. The use of diode forward drops for inserting a constant voltage drop is a common technique for voltage offsets inside integrated circuits, and a handy trick to have in your circuits "toolbox".

The second opamp is fed through a sensitivity pot from the output of the first. This control lets us adjust the scale of the final output envelope to take into account the variation in levels from signal sources. The second opamp's output feeds the amplified signal through another similar LED or diode string to subtract off the equivalent of the first bias voltage, and the then half wave rectified signal id dumped through a current limiting resistor into a capacitor filter. The capacitor voltage is then the output envelope. Note that the loading on the capacitor determines the speed of the capacitor voltage decline, and therefore both the size of the ripple in the envelope, and the speed that the capacitor can decline to follow sudden cut-offs in notes. Some envelope filters add an explicit loading resistor to control the decay time of the note as well. Even more elaborate filters than the single capacitor can be used as well.

The components in the dotted outline add a second and inverted half wave rectification, to give an effective full wave rectification if desired.

There are many ways to do a low voltage half or full wave rectifier/filter. This one is illustrated just because it's simple and easy to work with.

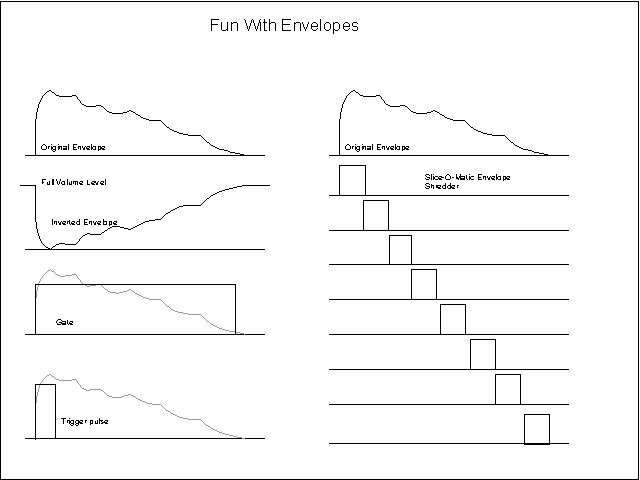Having spent all that effort getting an envelope signal, what good is it?

This is the fun part. You can do anything you're clever enough to design. For instance: the original envelope or its inverted version can be fed to a voltage controlled filter. This is what is done inside the Mutron III auto-wah filter. A simpler version is done by the Seamoon Funk Machine, the EH Dr. Q, and others.

A technique that's easy but not commonly known is to use some other signal to time-slice the envelope signal itself with some other signal. The envelope represents a kind of raw loudness signal. You could divide the basic guitar signal in a digital divider and use *that* to chop the envelope, so you'd have a bass octave down that has loudness that follows the original guitar's loudness more like a real bass. You could do the same for a phase locked loop note follower and generate thirds, fourths, fifths above and below the original signal that also follow the original guitar's signal loudness. Both of these techniques have been used in commercial pedals.

If you want to know when there's a note and when there's not, you feed the envelope into a comparator with a reference voltage just above zero. That makes a "gate" waveform that is high when the note is louder than the threshold. That can be the basis for a noise gate. It can also be used to turn on some other circuit for just the time the note sounds. By taking the "gate" waveform through a resistor to a capacitor to ground, the capacitor voltage would rise from zero toward the max gate voltage - it's an attack delay, with a rise speed controlled by the resistor. A little wave-shaping can also give you a trigger pulse that indicates when a note has just started.

The Slice-O-Matic envelope scheme lets you pick off the time periods when the loudness is between two levels.

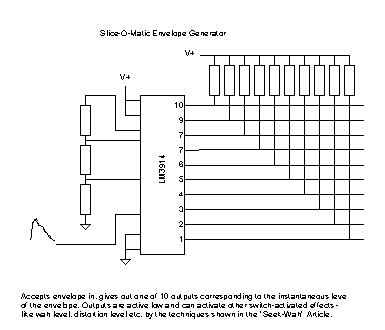This is one version of a Slice-O-Matic. The National Semi LM3914 has on-chip references and comparators to select one of ten outputs when the input voltage to the chip is at levels in the programmed range. Feeding an envelope signal into the chip gives up to ten output signals, each low during only a small portion of the envelope.

Here are some circuit ideas for using envelope information.

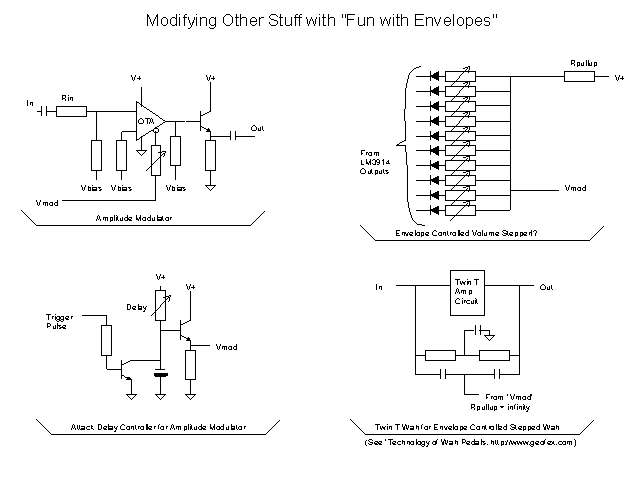The amplitude modulator is pretty much the variable gain section from a Dyna-Comp compressor, which was in turn lifted from an RCA application note for the CA3080. The gain of the modulator from input to output is linear with the amount of current going into the control pin, which is in turn controlled by Vmod divided by the variable resistance as shown. If you fed a solid sine wave into the input and fed a guitar note's envelope into the modulation input, you'd get a monotonous series of sine wave tones that were shaped like guitar notes. Dull.

But, if you instead fed the guitar's own signal into the modulator, and attached the attack delay circuit to the gain control, you would get a note that started with no gain, then ramped up as the capacitor to ground under the delay resistor charged it. In effect, you've rewired a Dyna-comp into an attack delay.

If you take the many outputs of the Slice-O-Matic circuit and connect them all through variable resistors to the capacitor junction of a Twin T wah, you get a stepped wah sound as each one is switched in and out.

Other applications that come to mind:

Use the trigger pulse to *stop* the oscillator of a simple tremolo, like the EAN Tremolo, using just the resistor and transistor from the attack delay module, you get a weird tremolo that always starts a note being off (no tremolo), and then the tremolo starts up as you hold the note.

The gate, envelope and reverse envelopes can turn on other sounds, like a noise generator, drone oscillator, anything else you want turned on.

We haven't touched the frequency part of note processing yet. There's some good stuff to mine there, too.