How it works...

Electricity

Electricity is formed from the motions of electrons. These are the tiny (even by atomic standards!) carriers of electric charge. Because protons, the carrier of the positive electrical charge, are thousands of times more massive and bound in the nucleus of atoms, only electrons carry electrical charge in the more normal sorts of electricity we all encounter. The charge on one electron is incredibly tiny, so it takes enormous numbers of electrons moving to have electrical effects that we see in our everyday lives. An ampere of current is the movement of about 6.25x10¹⁸electrons per second. A milliamp, which is a more normal size quantity for guitar effects, is one thousandth of that, or 6.25 x 10¹⁵electrons per second. This is important to us because if we get down to few numbers of electrons, things get "grainy" as the effect of the random distribution of a few electrons may not have a smooth variation. Some vacuum tube circuits have this problem, a form of quantization noise.

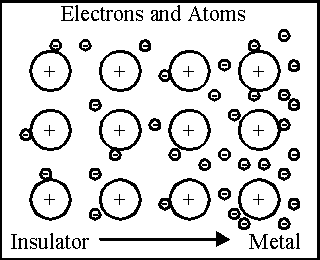
In the illustration at right, we see an illustration of the various kinds of atoms. At the left, the outer electrons are tightly bound to the atom. This is a characteristic of an insulator. On the right hand side, there are lots of free electrons that can move around within and among the atoms. This is a characteristic of a conductor. Usually the element displaying this are metals, and all the best conductors are metals. In the middle are materials which have some free electrons. These have various degrees of resistance to electrical flow.

We have special devices to make electrons flow. The most common is a battery. A battery is two metallic plates (conductors for good transfer of electrons) separated by some chemical gook. If we assume that the shaded areas marked with "+"'s and "-"'s are the metallic terminals of the battery, the atoms inside the battery between the two plates undergo a chemical reaction that forces electrons to one terminal of the battery and removes them from the other side.

We can think of a battery as an electron pump. The terminal with the excess of electrons is the (-) terminal and the one with a deficiency of electrons is the (+) terminal. Different mixes of chemicals have different amounts of "electron pressure" that they can exert. We call the "electron pressure" voltage. It's a measure of how hard electrons are being pushed to be somewhere else. Lead/lead sulfate and sulfuric acid batteries exert 2.2 Volts of force. Carbon/zinc/zinc chloride batteries exert 1.5V of force, as do alkaline cells. If we want more voltage/pressure, we stack a batch of cells up in series. A 9V battery is six carbon/zinc or alkaline unit cells in series in side one outer case.

Notice that the drawing is marked "Battery/Fuel Cell". A fuel cell is just a battery that you can feed more chemicals into continuously and so instead of the chemicals all getting used up and the battery drained, we can just pump in more chemicals and the thing will keep putting out electrons until the fuel supplies run out.

How many electrons can flow out of a battery or fuel cell at the same time depends on how big the surface area of the two plates is. In general, the more plate area, the more electrons can be pumped out at the same time. Remember, we call the number of electrons per second "current", so the bigger the battery, the more current it can supply. Because the chemicals inside the battery will have some resistance, there is a maximum current it can supply even if its (+) and (-) terminals are directly connected. The limit may be high, but it's there. More about this when we talk about resistors.

Some special batteries can be recharged by forcing electrons back in the (-) side and pulling them out of the (+) side. This state of affairs requires that the chemical reactions be completely reversible inside the battery. Nickel-cadmium batteries (1.2V/Cell) and lead-acid (2.2V/Cell) batteries do this well. Ni-Cads are the common hand held chargeable batteries, and lead-acid is the basis of car batteries. Some other types of batteries can not be recharged because the chemical reaction inside the battery is not reversible. Carbon-zinc batteries are like this, as are all types of fuel cells.

We can store electrons in a capacitor temporarily. A capacitor is kind of like a battery in that there are two metal plates separated by some insulator. There can be no electron flow between the plates in the sense of electrons actually moving across the insulator barrier. But if we put the plates very, very close together and pile up electrons on the (-) side and remove them from the (+) side by pumping them with a battery, the electrons piled up on the (-) side pull on the atoms with fewer electrons on the (+) side, setting up an electric field.

If we then disconnect the battery, the piled-up electrons have nowhere to go. They just sit there because they're insulated on all sides and can't flow. The voltage remains on the capacitor because the electrons have been pulled away from the atoms on the (+) side, and so this electron pressure exists. If we connect a conductive wire from the (+) side to the (-) side, the electrons now have a path, and they run around to the (+) side and neutralize things out; the capacitor discharges just like the battery did, but since it was just pressure piled up across the insulator, it runs out of electrons faster than a battery of similar plate area does. The battery has all these electrons stored in the chemicals, the capacitor has them stored by separation.

If you think about it, the energy is actually stored in the electric field, the pull the electrons have for the atoms in the opposite plate that have had electrons stripped off - kind of like stretching a spring.

Another interesting aspect of electricity you may have noticed. Electrons can be "caged up" by insulators. There needs to be a way for electrons to flow in a complete circle (hey! circuits!) for the common forms of electricity to work. A battery needs to be able to pump electrons from its negative to its positive terminal through wires, resistors, etc. If there is no conductive path around the battery, no electrons flow, at least not for long. Remember that we hooked a battery to a capacitor? Current flowed until there were enough electrons on the negative plate of the capacitor and enough electrons missing from the positive plate so that the voltage of the electrons there/missing equaled the battery's pumping voltage, then the flow quit. What happens if we then quickly reverse the battery that charged the capacitor? All of a sudden, the positive (electron hungry!) terminal of the battery is connected to a rich source of electrons and the negative (electron full) side is connected to the electron hungry plate of the capacitor. Bango! The battery sucks in electrons from the negative capacitor plate, pumps electrons into the positive plate, then further pumps the capacitor with electrons in the reverse direction to what it used to be.

If we keep reversing the battery quickly, we can make current flow rapidly back and forth. Instead of direct current (DC) we have alternating current (AC). So capacitors can conduct AC but not DC (at least not DC for very long).

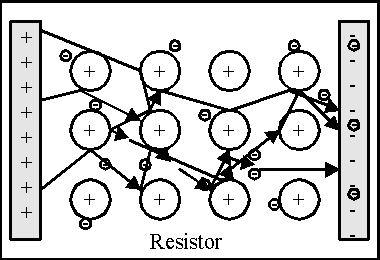But first - we gotta talk about resistors. A resistor is a material that is neither a good conductor nor an insulator for electron flow. What happens in a resistor is that there are some free electrons so they can still flow through, but the atoms and electrons are arranged in a way that electrons flowing through literally bump into the atoms already there. They may bounce off, or get captured permanently, or may stay a while and then move on to hit another atom. Each time an electron hits an atom, it imparts some energy to the atom, and the atom vibrates a little harder. We call electron vibration in solids heat - the electrons are actually making the material hotter by whacking into the atoms as they go through. As a result, we have to pump the electrons to force them through, and the pumping energy gets eaten up by the collisions and make the material hotter.

This is very important. For all common resistive materials, the pumping energy (voltage) is proportional to how many electrons go through (the current) in a linear way. We call the proportional constant the resistance, and this is measured in units of Ohms, after the fellow who discovered this.

An ohm is one volt of pressure per ampere of current flow. A thousand ohms (or K ohm) is one volt per milliampere.

Ohm's Law is one of the most fundamental things in electronics. It is entirely possible to have a career in electrical engineering with no other skills than an adroit application of Ohm's law. I've seen it done. So - MEMORIZE THIS!!! IN ALL THE POSSIBLE PERMUTATIONS!!!!

Resistance = Voltage divided by Current => R = V/I

Voltage = Resistance times Current => V = I*R

Current = Voltage divided by Resistance => I = V/R

It happens that we can express the energy that current flow leaves behind in any conductor of any kind, resistive or not, by multiplying the voltage across some bit of a circuit times the current flowing through it, or power in watts P = V * I

Using Ohm's law, we come up with some other very useful relations;

P = I²*R (by replacing V with I*R);

P=V²/R (by replacing I with V/R)

Just as you might think, the dimensions of the chunk of resistive material have something to do with the resistance. A short, wide block of resistive material has a lower resistance than the same amount of material squeezed into a long, skinny shape. Each material has a resistivity, or how much resistance it has per unit chunk of stuff; an actual resistor has length, width, and depth. The resistance is linearly dependent on the resistivity (given the symbol rho) and inversely dependent on the area of the material, so resistance R = (rho)*l / (area). "Rho" is the way you pronounce the Greek letter that sounds like "R", so it's a fancy say of saying "R for Resistivity" and leaving us the English "R" for the actual resistance.

Magnetic fields have this odd relationship with electrical charges. It happens that there can be no electrical current without causing a magnetic field, although there can be a magnetic field without current. We've already seen that electrons cause electrical fields when positive and negative charges are separated. Opposite electrical charges attract; like electrical charges repel, so electrons like to stay as spread out as possible.

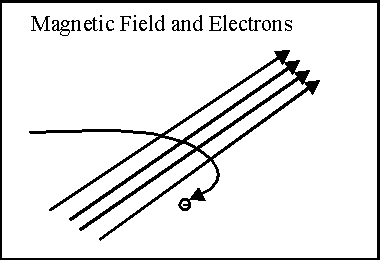
Magnetic fields neither attract nor repel electons - they make them move sideways! And the electron has to be moving for this to happen. Imagine that the diagonal arrows in the illustration at the right are a portion of a magnetic field. If we shoot a single electron into this field, the electron is deflected sideways across the magnetic field. If the field is strong enough, the electron can actually be curled into a spiral or circle.

This has some very odd consequences that you almost certainly have heard of.

For instance - what happens if we have a portion of a magnetic field and a wire through it that carried a current? The electrons are moving through the magnetic field, and they experience the same force that they would if they were in free space.

What happens is that they are forced to one side of the wire. In the illustration, imagine that the blue lines are a part of a magnetic field and that the electrons are flowing into the page. The edge of the wire is an insulating no-electron zone, so they're trapped in the wire. As you might expect, they start pulling the wire with them. The wire experiences a mechanical force that pushes it in the direction the electrons want to go. This is a real, measurable effect, and in fact is a classical experiment in freshman physics. It's also the basis of all electrical motors and relays.

There's another consequence of this effect. Remember when we talked about resistors, how the total resistance was R =(Rho)*l/Area? If a magnetic field is forcing all the electrons to one side of a wire, doesn't that mean that the area of the wire that is effective in conducting electrons has gone down, and therefore the effective resistance has gone up?

It absolutely does. This is kind of a "garden hose effect", where the resistance of a wire is increased by its being in a magnetic field. The amount of the effect is important in some transformer design; however, in some resistive materials, we can measure the voltage across the width of a strip of conducting material and actually measure the amount of electrons bunched up there as a result of a magnetic field. This is called the Hall Effect, and is the basis of a number of magnetic field detectors.

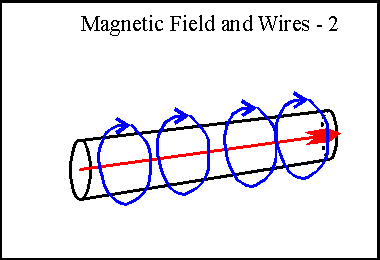Remember I said that current and magnetic fields are intimately related. Any time an electron moves, it causes a magnetic field to happen. The only way that this field could not make the electron curl up in little spirals is if the field is wrapped around the electron - and that's exactly what happens. Imagine that the red arrow in the illustration is a current flow, electrons moving through the wire. The resulting magnetic field will be wrapped around the wire in closed loops, as shown in blue. Magnetic field lines have the property that they are always a completely closed loop and are additive. It's possible to cancel out a magnetic field with an equal and opposite direction field.

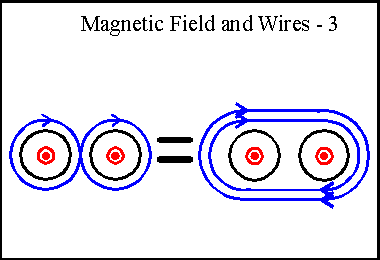
If we have two wires side by side, with the same current flowing through each one, the two magnetic fields are equal but opposite in the area between the two wires. However, on the outside of the two wires, they are equal, but add in strength, so the effect is of having one field of twice the strength circulating outside both wires.

Inductors

Resistors in series

Resistors in parallel

Voltage dividers

Thevenin and Norton

Voltage and Current Sources

Impedance - capacitive reactance and inductive reactance

Resonance and damping

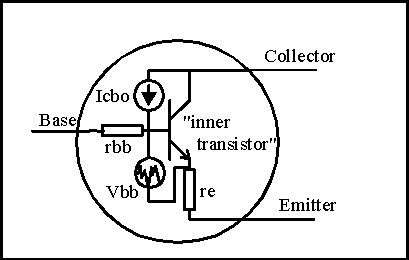
Transistors

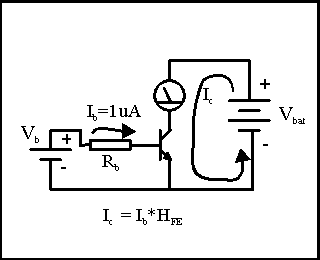Imagine that we set up an NPN transistor, a current meter and a battery as shown in the illustration. We hook this up so we can measure the battery current, connect the battery, and then look at the current meter. If the transistor is good, the current meter will read zero. This is because transistors are made to completely block current flow unless there is some current flow into the base terminal of the transistor. We've shown this with the little arrow indicating that Ib=0.

If we set up a second battery to supply some base current, and put in a resistor to set a fixed limit on that base current, we can measure the amount of current that flows per unit base current. Let's say that we use resistor Rb to allow 1 micro-amp (1uA) of base current to flow through the base-emitter of the transistor. We read the Ic current meter and find that we have 500uA of collector current flowing. The transistor is providing us with a gain of 500. This current gain is often referred to as Hfe.

For more fun, let's put a switch in series with Rb. If we click the switch back and forth, the transistor turns on and off. We can show this diagrammatically like this:

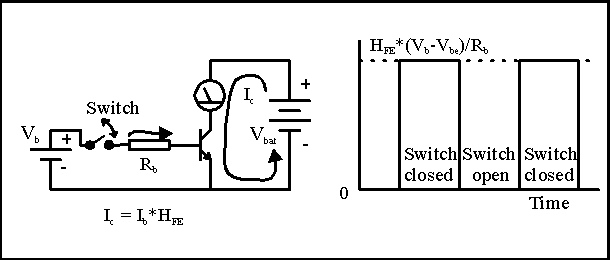
Notice that when the switch is on, the current is limited to the amount of current into the base times the current gain of the transistor, Hfe. Since we now know Ohm's Law, we can calculate the currents. With the switch closed, the voltage across the resistor Rb is the difference between the Vb battery and the voltage at the base. With the emitter grounded, we can call the base voltage Vbe for "voltage from base to emitter". So the actual voltage if we connected a voltmeter just across Rb is Vb-Vbe. The current that flows into the base MUST be (Vb-Vbe)/Rb. So by changing Rb we can set the value of the base current, and therefore set the collector current, because the collector current is just Hfe times the base current, or

Ic = Hfe* (Vb-Vbe)/Rb

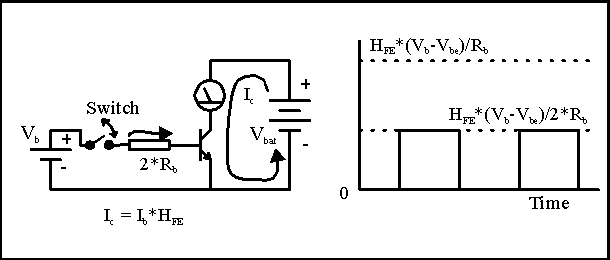
So let's change Ib. It is a quirk of bipolar transistors that Vbe is almost constant. So if we double Rb, the base current Ib is about half of what it used to be - Ib = (Vb-Vbe)/2*Rb. The illustration shows that the resulting collector current is also halved.

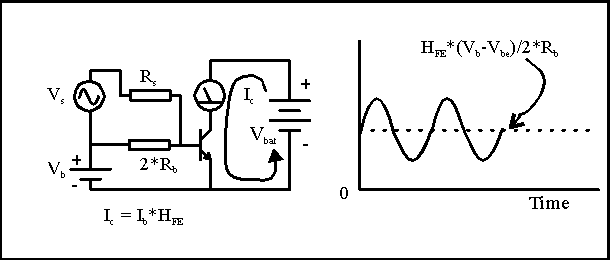
Instead of throwing a switch, let's add an alternating current (that is, swings positive and negative, also called "AC") signal to the base by hooking in an AC signal source, shown by the circle with the squiggle in it. We'll convert this voltage source to a current by running it through its own separate resistor, Rs. What we find is that the steady current from Vb and 2*Rb sets a bias point with the collector current set at some intermediate value. The current from Vs adds to the steady Ib on the positive half of the AC signal, and subtracts from Ib on the negative half, so the collector current shows the same wiggles as the Vs voltage, with different unit, as it is a *changing current*, not a *changing voltage*.

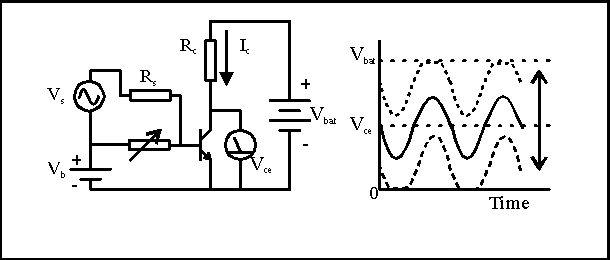
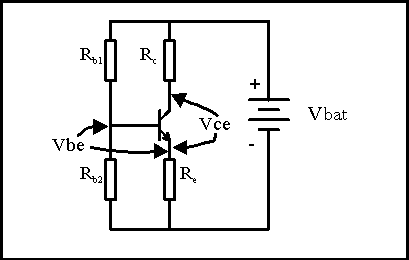
We also know from Ohm's Law that a resistor makes a fine current meter - the voltage across it is just the resistor value times the current. so let's put in a resistor instead of that current meter. If we were to measure the voltage just across the collector resistor Rc, we would find that the voltage exactly mimics what we saw from the current meter. But almost all electronics is done with only one reference point, called a ground point, so it would be more convenient to measure the voltage from the same point we have referenced the Vb and Vbe to. If we do that and measure the voltage from the collector to the emitter (Vce) we find that the collector current through the collector resistor eats up some of the voltage from Vbat, and we are left with Vbat-Ic*Rc across the transistor. This gives us the result that the voltage signal at the transistor collector is inverted compared to Vs. So transistor operation in this hookup gives an inverted voltage signal compared to the input signal. Notice that the emitter is common to both the input and the output circuit. Not much imagination is needed to name this a "Common Emitter" transistor circuit - and that's what it's called.

I've added one more wrinkle. Remember that changing Rb lets us change the collector bias point? Let's make Rb a variable and see what happens.

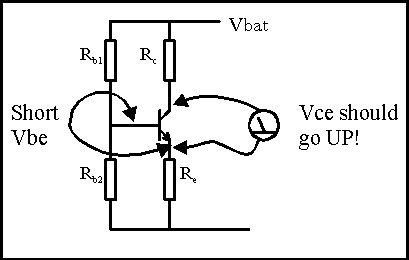
When we lower Rb, allowing a lot more current into the base, the no-signal collector current goes up. This makes the voltage drop across Rc larger, and leaves less of the Vbat voltage left for Vce. So the Vce bias point moves down towards 0Volt (because this circuit inverts the voltage) and the Vs signal just rides along. What happens when there is so much current going into the base with the sum of the static Ib current and the signal current from Vs that Ic*Rc is equal to Vbat? There is no more battery voltage left for the current in Rc to increase, so Vce hits 0 voltage and flattens out- there isn't any more voltage left for it go negative. The negative-going output signal is "clipped off" on the bottom.

Likewise, if we increase Rb so the Vce bias point moves up (lower current in Rc, so the collector is closer to Vbat), the signal current can at some point try to pull current backwards out of the base. It's a quirk of transistor construction that we'll see later that this can not happen, so the base current goes to zero. That forces the collector current to go to zero, and there is then zero voltage drop across the Rc resistor. The transistor is temporarily turned off, so the Vce is just equal to the battery voltage, and the signal is again clipped off, this time on the positive going output.

The clipping at the lowest Vce is called saturation because the transistor is already pulling all the current the rest of the circuit will let it have. The clipping at the highest Vce is called cutoff because the transistor current is cut all the way to zero. In between is the active or linear region.

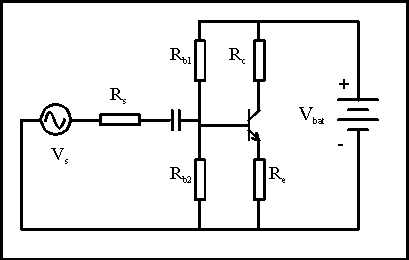
It's a pain to always have to use two batteries to run a transistor, so clever engineers have come up with several ways of doing this with only one battery. If we split Rb into two pieces, Rb1 and Rb2, and string them between Vbat and ground, it makes a voltage divider. The voltage at the center of the voltage divider is Vbat * Rb2/(Rb1+Rb2). Clearly, there is some resistance in series with the base from Vbat. If you do the math, the base "sees" a voltage that looks like a battery with a voltage of Vbat * Rb2/(Rb1+Rb2) through a resistance that is the parallel combination of Rb1 and Rb2. So by using one additional resistor and rearranging things a bit, we have the very useful result that we only need one battery.

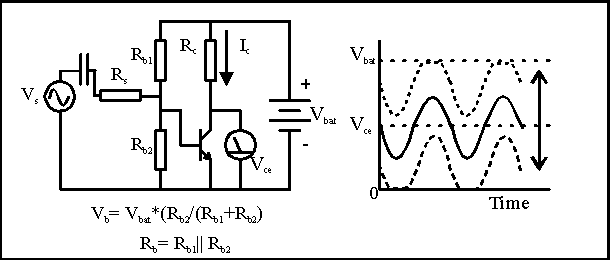
There are actually several ways to bias transistors, different arrangements of resistors that will leave the transistor conducting some current, and not at its cutoff or saturation points.